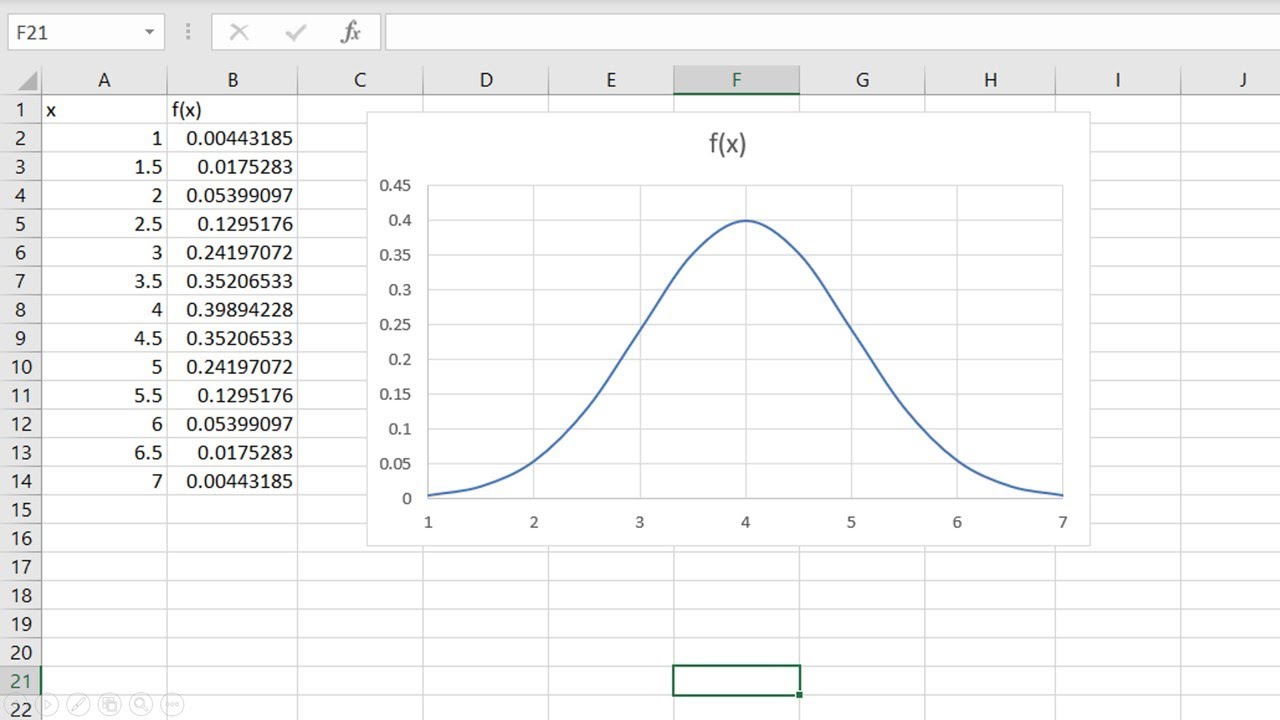
Imagina un gráfico que representa la distribución de un conjunto de datos, donde la mayoría de los valores se agrupan alrededor de un punto central y se dispersan simétricamente hacia los lados. Esta representación gráfica es conocida como la distribución normal.
El Fenómeno de la Distribución Normal
Cuando observas la grafica de una distribución normal, te enfrentas a un fenómeno fascinante en el mundo de la estadística. La distribución normal, también llamada la distribución gaussiana en honor al matemático Carl Friedrich Gauss, es un patrón que se encuentra en innumerables aspectos de la naturaleza y en datos recopilados en diversas disciplinas.
Propiedades Destacadas
Una de las propiedades más impactantes de la distribución normal es su forma de campana, que se asemeja a la silueta de una campana. Este patrón simétrico revela que la media, la mediana y la moda de los datos son idénticas, lo que enfatiza su centralidad en torno a un valor medio. Además, aproximadamente el 68% de los datos caen dentro de una desviación estándar de la media, y el 95% dentro de dos desviaciones estándar, lo que demuestra la previsibilidad de la distribución.
Aplicaciones en Diversos Campos
Desde la biología hasta la economía, la distribución normal se presenta de manera constante. En biología, las características como la altura de las plantas suelen seguir una distribución normal; en economía, los precios de mercado pueden comportarse de esta manera. Comprender la distribución normal es crucial para interpretar datos y tomar decisiones fundamentadas en diferentes áreas del conocimiento.
Características Relevantes de la Grafica
Al observar detenidamente la grafica de una distribución normal, notarás que la curva es suave y continua, sin puntos bruscos ni discontinuidades. Esto indica la fluidez y cohesión de los datos en su disposición alrededor de la media. La simetría de la campana revela que los valores tanto a la izquierda como a la derecha de la media son equidistantes, lo que significa equilibrio en la distribución de los datos.
Interpretación Visual
¿Te has preguntado por qué la grafica de una distribución normal se asemeja a una campana? La razón radica en la naturaleza misma de la distribución de los datos, donde la mayoría se concentran en torno a la media y disminuyen a medida que nos alejamos. Esta forma característica permite una interpretación visual inmediata de cómo se distribuyen los valores y qué tan dispersos están.
Existencia en la Naturaleza
La distribución normal es un fenómeno recurrente en la naturaleza, desde la forma de las nubes hasta la distribución de tamaños de partículas en un medio. Al observar la grafica de una distribución normal, conectamos con patrones que subyacen en la estructura misma de nuestro entorno y comprendemos la regularidad inherente a muchos procesos.
Importancia en el Análisis de Datos
En el ámbito del análisis de datos, comprender la distribución normal es fundamental. Nos permite realizar predicciones, identificar valores atípicos y realizar inferencias sobre la variabilidad de los datos recopilados. La presencia de una distribución normal indica estabilidad y nos proporciona herramientas para realizar comparaciones significativas entre diferentes conjuntos de datos.
Uso en Estudios Experimentales
¿Cómo se utiliza la distribución normal en estudios experimentales? Al analizar los resultados de un estudio, los investigadores a menudo recurren a la distribución normal para determinar la probabilidad de ciertos eventos, calcular intervalos de confianza y evaluar la consistencia de los datos obtenidos. Esta herramienta estadística es esencial para validar hallazgos y tomar decisiones informadas.
Aplicaciones Avanzadas
En campos como la inteligencia artificial y el análisis predictivo, la comprensión profunda de la distribución normal es crucial. Al modelar fenómenos complejos, los algoritmos a menudo asumen una distribución normal de los datos para realizar predicciones precisas y optimizar el rendimiento. Esta aplicación demuestra la versatilidad y relevancia continua de la distribución normal en disciplinas vanguardistas.
Futuro de la Investigación en Distribuciones
Ante la creciente complejidad de los datos recopilados en la era digital, la investigación en distribuciones, incluida la distribución normal, se torna aún más relevante. La exploración de nuevos modelos y técnicas para analizar la variabilidad de los datos y capturar su estructura subyacente se convierte en un desafío apasionante para matemáticos, estadísticos y científicos de datos.
Innovación y Desafíos
¿Qué innovaciones podemos esperar en el campo de las distribuciones? A medida que avanzamos hacia la era del big data, surgen desafíos en la gestión y análisis de conjuntos de datos masivos. La innovación en algoritmos y métodos estadísticos nos permitirá abordar estos desafíos y extraer información valiosa de los datos, incluso en contextos de alta dimensionalidad y complejidad.
Integración Multidisciplinaria
La integración de conocimientos y técnicas de campos diversos, como la informática, la matemática y la ciencia de datos, impulsará la investigación en distribuciones hacia nuevas fronteras. Al combinar enfoques interdisciplinarios, podemos abordar problemas complejos y descubrir patrones ocultos en los datos que de otro modo permanecerían invisibles.
¿Por qué se utiliza la distribución normal en tantos contextos diferentes?
La distribución normal se utiliza ampliamente debido a su presencia natural en muchos fenómenos y a sus propiedades estadísticas que facilitan la interpretación y predicción de datos. Su simetría y centralidad la convierten en una herramienta poderosa en diversas disciplinas.
¿Cómo se relaciona la distribución normal con otros modelos estadísticos?
La distribución normal sirve como base para muchos otros modelos estadísticos y es fundamental en la teoría de probabilidad. Muchos métodos estadísticos se apoyan en la distribución normal como supuesto subyacente para realizar inferencias y tomar decisiones.