La distribución de probabilidad normal: ejemplos
Entendiendo la distribución de probabilidad normal
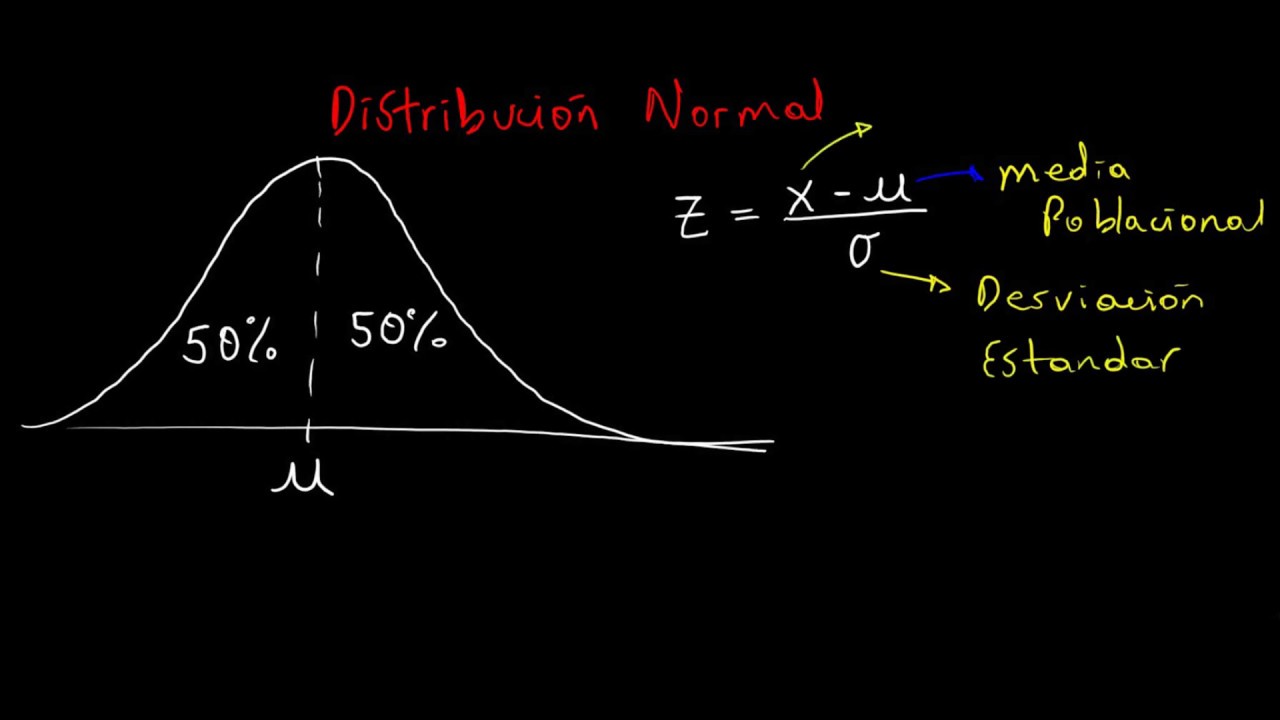
La distribución de probabilidad normal, también conocida como la distribución gaussiana, es uno de los conceptos fundamentales en estadística y matemáticas. Se caracteriza por ser una distribución simétrica alrededor de su media, lo que la convierte en un modelo probabilístico muy relevante en diversos campos.
Características de la distribución normal
Una de las principales características de la distribución normal es que sigue una forma de campana, con la mayor concentración de datos alrededor de la media y una dispersión que disminuye a medida que nos alejamos de ella. Esta distribución es continua y tiene un rango que va desde menos infinito hasta más infinito.
Importancia en la inferencia estadística
En el contexto de la inferencia estadística, la distribución normal desempeña un papel crucial. Permite realizar estimaciones, realizar pruebas de hipótesis y modelar fenómenos naturales y sociales. Su comportamiento predecible y bien entendido la convierte en una herramienta fundamental en la toma de decisiones basadas en datos.
Ejemplos de aplicaciones de la distribución normal
Economía: modelado de variables financieras
En economía, la distribución normal se utiliza ampliamente para modelar variables financieras como rendimientos de activos, precios de acciones y tasas de interés. Esto permite a los analistas y traders comprender mejor el comportamiento de los mercados y tomar decisiones informadas.
Salud: análisis de datos clínicos
En el campo de la salud, la distribución normal es clave en el análisis de datos clínicos, como la distribución de pesos de una población o la variabilidad de la presión arterial. Ayuda a los profesionales de la salud a interpretar los resultados de estudios y a tomar decisiones médicas basadas en evidencia.
Calidad: control de procesos industriales
En la industria, la distribución normal se utiliza en el control de calidad de procesos para garantizar que los productos cumplan con ciertas especificaciones. Permite identificar desviaciones significativas en la producción y tomar medidas correctivas de manera oportuna.
Usos avanzados de la distribución normal
Teoría de la probabilidad: teorema del límite central
En teoría de la probabilidad, la distribución normal surge como resultado del teorema del límite central, que establece que la suma de un gran número de variables aleatorias independientes tiende a una distribución normal, independientemente de la distribución original.
Estadística bayesiana: distribuciones a priori y a posteriori
En estadística bayesiana, la distribución normal se utiliza como una distribución a priori o a posteriori en la estimación de parámetros desconocidos. Esto permite incorporar información previa en el análisis y actualizar nuestras creencias con nueva evidencia de manera coherente.
La distribución de probabilidad normal es una herramienta poderosa y versátil que se aplica en una amplia gama de disciplinas. Su comprensión es fundamental para cualquier persona que trabaje con datos y busque obtener información significativa a partir de ellos.
¿Por qué la distribución normal es tan comúnmente utilizada en estadística?
La distribución normal es ampliamente utilizada en estadística debido a su simplicidad y a que muchos fenómenos en la naturaleza siguen este patrón de distribución, lo que facilita su aplicación en diferentes contextos.
¿Cómo se relaciona la distribución normal con el concepto de desviación estándar?
La desviación estándar en la distribución normal representa la medida de dispersión de los datos alrededor de la media. Una desviación estándar mayor indica una mayor dispersión de los datos, mientras que una menor indica una concentración más cercana a la media.
¿Existen casos en los que la distribución normal no sea adecuada para modelar un conjunto de datos?
Aunque la distribución normal es muy útil en muchos casos, existen situaciones donde otros tipos de distribuciones, como la distribución t de Student o la distribución exponencial, pueden ser más apropiadas para modelar ciertos fenómenos con características específicas.