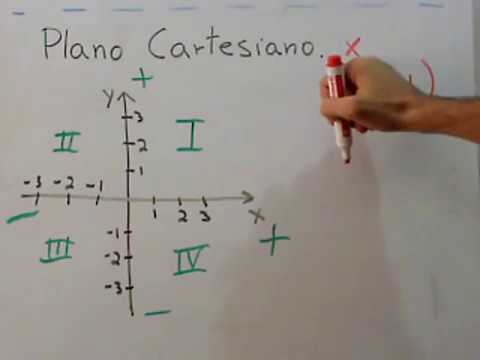
Los cuadrantes en un plano cartesiano son fundamentales para la ubicación de puntos y el estudio de funciones. Se dividen en cuatro secciones, cada una con características y signos particulares que los hacen únicos.
Explorando la Importancia de los Cuadrantes
¿Qué son los Cuadrantes?
Los cuadrantes son las divisiones que se encuentran en un plano cartesiano y permiten identificar la posición de un punto utilizando coordenadas. ¿Te imaginas navegar sin un mapa detallado que te guíe?
La Distribución de los Cuadrantes
Los cuadrantes se distribuyen de forma ordenada, numerándose en sentido antihorario comenzando desde el cuadrante I en la esquina superior derecha. Similar al giro de las manecillas del reloj, ¿cierto?
Los Signos en los Cuadrantes
Cada cuadrante posee un conjunto de signos para las coordenadas, positivos o negativos, que indican la dirección en la que se ubican los puntos. ¿Son como las señales que nos indican la dirección en una encrucijada?
Características de cada Cuadrante
¡Los cuadrantes tienen personalidades únicas! Desde el primer cuadrante hasta el cuarto, cada uno alberga particularidades que influyen en la representación gráfica de los puntos.
Cuadrante I: Positivo en ambas coordenadas
El cuadrante I es el hogar de los puntos con coordenadas positivas tanto en x como en y. Es como estar en una esquina soleada, ¿verdad?
Cuadrante II: Negativo en x, positivo en y
En el cuadrante II, las x son negativas pero las y siguen siendo positivas. ¿Te recuerda a esos días lluviosos que traen brillo al final?
Cuadrante III: Negativo en ambos ejes
¡El cuadrante III es muy fresco! Aquí tanto x como y son negativas, creando una zona diferente pero igual de importante en el plano. ¿Como un oasis en medio del desierto?
Cuadrante IV: Positivo en x, negativo en y
Finalmente, el cuadrante IV combina x positiva con y negativa. Es un espacio que equilibra lo contrario, ¿cómo un dulce y salado en la gastronomía?
Aplicaciones Prácticas de los Cuadrantes
Comprender los cuadrantes es esencial en diversas áreas, desde matemáticas hasta navegación, brindando un marco de referencia para ubicar lugares y analizar datos de manera eficiente.
Matemáticas y Funciones
En el mundo de las funciones matemáticas, los cuadrantes son esenciales para representar gráficamente ecuaciones y visualizar cómo varían con respecto a los ejes. ¿Como un lienzo para un artista?
¿Cómo se Representan las Funciones en los Cuadrantes?
Las funciones pueden tener diferentes comportamientos en cada cuadrante, lo que permite analizar su concavidad, crecimiento o decrecimiento en segmentos específicos. ¿Son los cuadrantes como escenarios cambiantes para las funciones?
En el ámbito de la navegación, los cuadrantes se utilizan para determinar la posición de un objeto en un sistema de coordenadas definido. ¿Como seguir un mapa para encontrar un tesoro escondido?
¿Cómo se Calculan las Coordenadas en los Cuadrantes?
Cada cuadrante tiene reglas específicas para asignar valores a las coordenadas, lo que facilita la identificación precisa de ubicaciones en un plano. ¿Similar a seguir las instrucciones de un GPS para llegar a un destino?
Los cuadrantes en un plano cartesiano no solo son divisiones geométricas, sino herramientas útiles que nos guían en la representación gráfica y la ubicación precisa de puntos en un sistema coordenado.
¡Explora y Domina los Cuadrantes!
¡Aventúrate a través de los cuadrantes y conviértete en un experto en la geografía matemática del plano cartesiano! ¿Dispuesto a conquistar este mapa?
¿Por qué son importantes los cuadrantes en un plano cartesiano?
Los cuadrantes brindan una estructura visual que facilita la ubicación de puntos y la representación gráfica de funciones matemáticas.
¿Qué sucede si un punto se encuentra en los ejes del plano cartesiano?
Los puntos ubicados en los ejes x o y se consideran especiales, ya que su coordenada opuesta es siempre cero, lo que les confiere características particulares en el sistema de coordenadas.
¿Se pueden aplicar los cuadrantes en otras disciplinas fuera de las matemáticas?
¡Absolutamente! Los cuadrantes se utilizan en campos como la navegación, la geolocalización y la física, donde la representación gráfica de datos es fundamental para la comprensión y el análisis de fenómenos.